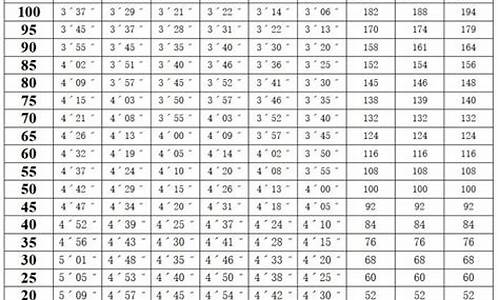
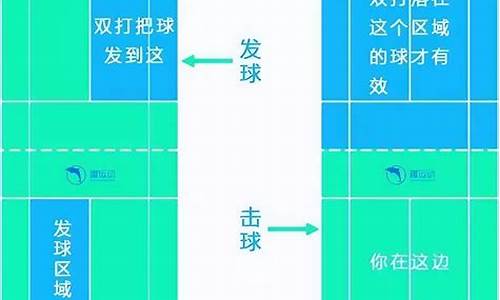
羽毛球比赛计分规则中单局比赛率先得到分为胜_羽毛球比赛率先得到多少分的一方赢得单局比赛

1.能帮忙解决数学问题

2.你是否了解怎么看羽毛球比赛？需要注意什么？

3.征求2003年中山大学数学建模B题的报告论文(答案)

一种独特的古老体育运动项目，它有着悠久的历史。运用自己的脚腕、膝关节等同时夹、顶球，不让球落地，类似我国民间踢花毽子。藤球跟排球比赛有些类似，所不同的是以脚代手，所以又叫“脚踢的排球”。 项目：藤球

亚运小项 ：

男子：单组赛、团体赛、圆场赛

女子：单组赛、团体赛、圆场赛

藤球是用9~11根细藤单曾藤条编制而成的**空心圆球。球的周长是53厘米。球的直径约12厘米，球面上有12个五角形孔。重量为160~180克。藤球是一种介于排球、篮球、足球之间的运动。

藤球运动是两队隔网竞赛的运动，是一项观赏性、竞技性很强的项目。藤球的体积小、重量轻，要用脚去支配和控制球，但技术动作比足球更加精确、高难。藤球是流行于东南亚泰国、缅甸、马来西亚、新加坡等地区的一种独特的古老体育运动项目，它有着悠久的历史。运用自己的脚腕、膝关节等同时夹、顶球，不让球落地，类似我国民间踢花毽子。藤球跟排球比赛有些类似，所不同的是以脚代手，所以又叫“脚踢的排球”。

藤球是一项技巧性很高的运动，在“传”球时要运用特殊的技术。藤球是在一块手织机编织铺就的场地内进行。每支球队上场2~3人。击球过网，并使球落到对方场地内，或使对方球员接球出界。藤球的基本动作——踢球，通常需要将脚踢到半空齐肩的高度。在马来语(藤球发源于马拉西亚)中，踢球称为“sepak”，运球称为“takraw”。藤球运动员不许用手触球。在比赛中，他们可以用脚、腿、肩膀和头来触球。为了使球保持在空中飞行，运动员需要使用停球、各种杂技式的动作或踢球等方法。

[编辑本段]

项目历史

[藤球运动]

藤球运动

藤球运动源于15世纪的苏丹国统治下的马六甲一带地区，由马来西亚的“sepak raga”运动发展而来。当时，人们在劳动之余，围成一圈，不用手和胳膊，用头顶球、用脚踢球，使之不落地，传踢一个藤球(raga)，使其在空中停留尽量多的时间。

这种轻松愉快、消除疲劳的运动很快便在东南亚一些国家传开了。缅甸、马来西亚、泰国和新加坡等国开展得较好。尔后，它又迅速地传入印度、菲律宾及马来西亚等地。早在11世纪，东南亚国家文化中就有关于藤球运动的记录。泰国开展这项活动已经有几百年时间了。在缅甸，700多年前的蒲甘王朝时就相当盛行。在泰国，它被称为“takraw”，在菲律宾称为“sipa”，在马来西亚、新加坡和文莱成为“sepakraga”，在缅甸称为“ching loong”，在印度尼西亚和老挝称为“rago”。

自从东南亚的爱好者们加入球网并制定了类似排球的规则之后，藤球比赛变得更激烈，挑战性更强了。1945年在马来西亚的槟榔屿举行了一场藤球表演赛，引起了巨大反响。此后，藤球运动如燎原之火传遍了马来半岛和东南亚各地。1960年，一套完善的比赛规章制度建立起来。这项运动被定名为藤球(sepaktakraw)，并进入了东南亚运动会。

现代藤球的产生仅有40多年的历史。它是以藤球运动中网的使用为标志的。泰国前教育部长科·乔哈利对推广藤球运动作出了一定贡献，被认为是“现代藤球运动之父”。乔·哈利经过努力，使藤球于1965年被正式列为两年一度的东南亚运动会的正式比赛项目并开始在东南亚国家中流行起来。1982年藤球作为表演项目进入亚运会，并被列入1990年北京亚运会正式比赛项目。中国藤球运动发展较为缓慢。1987年底，亚洲藤协率队来华访问表演，精彩的表演赛令众多中国观众大饱眼福。这次访问对我国的藤球发展起了很大的促进作用。从此中国也开始这方面的练习，并开始介绍并推广这项健体强身的竞技运动。

[编辑本段]

场地设施

藤球要求

①构成：藤球是用9--11根细藤单曾藤条编制而成的**空心圆球。

②周长：球的周长是53厘米。

③直径：球的直径约12厘米。

④形态：球面上有12个五角形孔。

⑤重量：重量为160--180克。

场地要求

①场地：面积为13．4米×6．1米，在8米空间内不得有障碍。

②边线：场地所有边线的宽度从内侧量起不得宽于0．04米。场地之间、场地与障碍物之的缓冲距离为0．9米到1．8米。

③中心线：宽度0．04米的中心线将场地分成相等的左右两个部分。

④1／4圆：在场地中心线的角上，边线与中心线交接处各有两个半径为0．9米的四分之一圆，宽度为0．04米的边线将从一圆的外测量起。

⑤发球圈：在左右场各有一个半径为0．3米的发球圈。其圆心距离底线2．45米，距边3．05米，宽度为0．04米的线，应从发球圈的外测量起。

网柱要求

①网柱：网柱应高于地面1．55米，应加以固定以便将网拉紧。网柱需由坚硬的材料制成，其半径不得大于0．04米。

②网柱的位置：网柱应固定在边线外0．3米处，与中心线成直线。

网的要求

①网由普通细绳或尼龙绳制成，网孔为0．04米至0．05米之间。网的宽度为0．7米，长度不得超过6．11米。网的上、下端需用带子包边，宽度均为0．05米，以便穿绳将网拉紧平于网柱顶端。网的中部上端高1．52米，靠近网柱的两侧高为1．55米。

②标志线：如果网超过尺寸，则在网的两端使用可松动的、宽度为0．05米的带子，并与两侧进线和中心线垂直。

[编辑本段]

规则介绍

“regu”是马来语。在正式赛事中，藤球比赛分为3项，单组赛、双人赛和团体赛。

[藤球比赛中]

藤球比赛中

单组赛：每支球队上场3人，并有2名替补。

团体赛：每支球队每个regu3人，共3班，即9人，并有3名替补。

双人赛：每个regu2人，并有1名替补。

单组赛和团体赛

发球者(feeder)或击球者(striker)将球投给接球者(server)，接球者必须一只脚站在圈内，另一只脚将球踢出。即使球触网或落在场地内都可得分。如果得分，比赛将继续进行。在比赛中每方只有3名球员在场上，但可以随时增加1名替补。如果使用了1名替补，那么在比赛进程中将不得使用其他替补了。在团体赛中，比赛与单组赛程相同，但每支球队都有3个单组，总共可有12名队员参赛。每队的第一组将进行3局比赛，获胜的组为本队得1分。第二组之间的胜者仍可为本队得到1分。如果有一支球队在前两组比赛中都获胜，第三组之间的加赛就不需要再进行了。

双人赛

每队由两组选手进行比赛，每组2名运动员。其中一人是后卫，位置在后场，负责发球和接球，他可以在基线后的任何位置发球，被称为“tekong”。另一名球员也被称为“alternate tekong”，负责运球，他和后卫也都可在各自的位置上接球。每得一分，运球的两名球员位置就相互轮换一次，直到有一方得分超过规定数字。在比赛进行中，每方只允许有有2名球员在场上，但随时可以有1名替补上场。在整场比赛中，对替补的使用没有限制。

得分系统

一方踢球过网，使对方经3次传递都无法回球过网，或迫使对方回球出界，就可得分。无论谁发球，任何一方只要该球获胜都可得分。只要有得分，就换发球。当发球一方或接发球一方出现失误，对手得分，并换发球。每场比赛进行2局。每局21分制，如果出现20比20的平局，一方要超过对方2分才可获胜，最高分值为25分。如果两个组各赢一局，那就需要加赛一局，称为“决胜局”(tiebreak)，决胜局只有15分，当为14比14平，一方要超过对方2分才可获胜，最高分值为17分。

[编辑本段]

运动特点

藤球是一项很高技术的项目，要求用特殊的技巧来处理球。一般每支参赛队拥有2名到3名的队员，得分主要依靠在用脚将球踢到对方场区（球场大概是羽毛球球场大小）内，而对手无法救起。

踢，是特球比赛的主要动作，他要求在半空中踢球的位置至少达到肩的高度。“sepak”是马来西亚语，为藤球的专业用语“踢”的意思。藤球比赛中，选手不能用手，他们能够用脚，腿，肩和头触球。选手常常在藤球比赛中有非常高难度带杂耍意味的动作来控制球的运行。在早期，藤球比赛是一个用大家在玩一个用藤条做成的球，他们尽力不用手或者手臂触球，但是使得球不落地。随着比赛规程的日益完善之后，成为了队制的比赛。 “Regu”是马来西亚语中球队的意思。比赛有3种类型：

[踢球]

踢球

－ 单组赛（Regu Event）：4人（包括1名替补）

－ 团体赛（Team Event）：12人（包括3名替补）

－ 圆场比赛（Circle Game）：6人（包括1名替补）

－ 运动员的位置：三名选手中必须有一人在后场担任后卫（负责发球）。剩下的两名选手一人在左，一人在右。

在比赛开始时，双方运动员都必须回到各自的区域内做好准备。后位选手在发球时一只脚要站在发球区内，另外一只脚用来发球。发球方的其他队员要站在各自的区域之内。接发球方的队员可以站在己方场地的任何地方。在每局比赛中先得到15分的一方获胜，每局的中间休息2分钟。如果总局数打成1:1的话，则要进行决胜局的比赛，在决胜局中先得到6分的一方获胜。在决胜局中，任何一方得到三分时双方交换场地。在进行圆场比赛时，5名选手围成一个圆形进行10分钟的连续传球，在没有失误的前提下传球数最多的一方获胜。

藤球运动源于15世纪的苏丹国统治下的马六甲一带地区。当时，人们在劳动之余，围成一圈，用头顶球、用脚踢球，使之不落地。这就是现代藤球运动的前身。这种轻松愉快、消除疲劳的运动很快便在东南亚一些国家传开了。缅甸、马来西亚、泰国和新加坡等国开展得较好。尔后，它又迅速地传入印度、菲律宾及马来西亚等地。泰国开展这项活动已经有几百年时间了。在缅甸，700多年前的蒲甘王朝时就相当盛行。作为民间的体育活动，它犹如中国的踢毽子，可做出 各式各样巧妙、复杂的动作。在不同的国家，藤球的叫法不同。在泰国叫做“takraw”，菲律宾叫做“ sipa”。“sepakraga” 是马拉西亚、新加坡和缅甸的叫法，也成为了国际叫法。由于藤球比赛类似于排球的规则，但是更具有对抗性和竞争性，因此在东南亚地区非常流行。在1945年俄马来西亚的槟榔屿就已经开始举行比赛。1960年一系列的规则开始健全。

能帮忙解决数学问题

一.本届亚运会已经进行了两天，中国代表团已经夺得了20枚金牌，其中有很多精彩的夺金时刻。例如以下这几个：

1.孙杨在男子200米自由泳决赛中以1分44秒65的成绩夺冠，刷新了自己保持的亚洲纪录，并成为该项目连续三届亚运会的冠军。中国游泳队不仅席卷当日游泳赛场的全部7枚金牌，且在所有项目上都打破赛会纪录或亚洲纪录，并在4个项目上包揽金银牌。

2.中国赛艇队姑娘邹佳琪/邱秀萍在女子轻量级双人双桨决赛中以绝对优势夺冠，获得本届亚运会的首枚金牌。从2002年釜山亚运会至今，中国体育代表团从未让亚运会首金旁落。

3.值得一提的是，作为浙江“00后”的三小只此次比赛成绩打破了亚洲纪录。其中，黄雨婷还在女子10米气个人决赛夺得金牌，这也是中国队的第十枚金牌。中国射击队在女子10米气团体赛中获得冠军，夺得中国队的第二枚金牌。

二.以下是一些关于历届亚运会的举办地点和比赛结果的信息：

1.亚运会的前身是远东运动会，从1913年到1934年间，先后在菲律宾、中华民国和日本等地举办了十届。

2.第一届亚运会于1951年在印度新德里举行，有11个国家和地区的489名运动员参加了6个项目的角逐。日本以24金、20银、14铜的成绩位居奖牌榜第一名。

3.第十一届亚运会于1990年在中国北京举行，这是中国首次承办的规模最大的国际综合运动会。共举办了27种运动308项比赛，来自36个国家地区的4655名选手参加。中国以61金、51银、41铜的成绩位居奖牌榜第一名。

4.第十八届亚运会于2018年在印度尼西亚雅加达和巨港举行，这是亚洲历史上第一次由两个城市共同承办的亚运会。共举办了40种运动465项比赛，来自45个国家和地区的11752名选手参加。中国以132金、92银、65铜的成绩位居奖牌榜第一名。

5.第十九届亚运会将于2022年在中国杭州举行，这是中国继北京和广州之后第三次承办亚运会。预计将有40种运动462项比赛，其中电子竞技将首次成为正式竞赛项目。

总之，亚运会是亚洲最大的综合性运动会，有着悠久的历史和丰富的成就，届亚运会已经进行了两天，中国代表团已经夺得了20枚金牌，其中有很多精彩的夺金时刻。

你是否了解怎么看羽毛球比赛？需要注意什么？

乒乓球新旧赛制对析

关键字：11分制 21分制

题目描述：

自2001年10月1日起，国际乒联改用11分制等新规则。11分制的实行，使比赛偶然性增加，让一些二三流选手也有机会战胜一流选手。“但这个偶然性应有个度，”王家声说：“如果这个偶然性大到世界顶尖高手也纷纷被无名小卒淘汰，三四流选进决赛，那它就不是好规则了。”，是否会象羽毛球7分制一样实行不久就取消呢？

请就乒乓球新旧赛制对析，试对11分制的5盘3胜与21分制的3盘2胜制作定量的比较分析；试对11分制的7盘5胜和21分制的5盘3胜制作定量的比较分析；请就是否有利于运动的推广；是否有利于形成对抗激烈，场面精彩的比赛；是否有利于它的市场开发和赞助商利益方面来评价乒乓球11分制利弊如何，并作出建议。

参量和函数说明：

I 中的如下：

A：选手一 B：选手二

WA:A胜的球数 WB: B胜的球数

g: A每球的胜率，即赢得一球的概率

P1: 11分制下，A胜出一局，且WA=11,WB<10时，的概率

P2：11分制下，A胜出一局，且 WB>=10,WA=WB+2时，的概率

P3：11分制下，A胜出一局的总概率

P4：11分制下，5盘3胜，A胜出的总概率

P5：11分制下，7盘4胜，A胜出的总概率

p3: 21分制下，A胜出一局的总概率

p4: 21分制下，3盘2胜，A胜出的概率

p5: 21分制下，5盘3胜，A胜出的概率

II 中的如下：

A：选手一 B：选手二

i:A的得分，赢球数 j:B的得分，赢球数 n:总球数

g(i,j): A在i:j下胜出一球的概率，是随赛程而变化的函数

g0：A刚开始时的胜率

m(x):来表A进入状态的快慢程度对g造成影响的调谐因子

α:关键球(决胜负的一球)对A方对输赢此球的影响的因子

w(i,j)：用来描述A方输赢在i:j下，赢得此球的因子函数，当状态i:j时为可决定胜负(关键球)时w(i,j)=α，否则w(i,j)=1(也就是对比赛无影响)

L(x)：A输球数(输球数为负时，即赢球)对g的影响的因子函数，其中x=i-j

C：用来来标记A是否最先发球，若是则C=0，否则C=1

F(x)：发球权对A的胜率g的影响的因子函数，其中在11分制下x= mod(2) ，21分制下x= mod(2) 。

G(i,j)：到达i:j时的概率

L1：表示A胜的折线 L2：表示B胜的折线

P1：在11分制下，A胜出一局的概率 P’1：在21分制下，A胜出一局的概率

解答过程：

I,初步建模

我们不妨先建立一个两选手对战的模型，且作出以下规定：1,根据两选手的技术水平，给定他们每一球胜出的概率；2，设这种概率是恒定不变的，也就是说不考虑其它因素的影响。

现有两选手A和B对战，我们现在只拿出一个选手出来作考虑，比如A，因为比赛双方是相对的，确定了A的胜率，B胜率也随之确定(等于1减去A的胜率)。记A赢球为标志1，输球为标志为0，则概率空间X={0,1}。设比赛共打了n球，则由前面的设易知，存在服从0-1分布的n个相互独立的随机变数x1,x2,x3,…,xn ，其中xi∈X,i=1,2,..,n。

设A每球的胜率为g(相应地B的胜率为1-g)，对战n盘，有Y=X1+X2+…+Xn ,服从两项分布ψ(n,g).

一、现在我们先来讨论11分制下A选手胜出的总的概率。

由于在每一局中，只有当A先胜出B至少两球，且打足11球时，A方可赢得这一局。

这样说来，我们可分两种情况来讨论，一是A先胜出11球，且B胜出的不足10球，则A就可胜出了。二是，B超过或等于10球，这时当且仅当A领先出两球时，A才可赢得本局。

记A胜的球数为WA，B的为WB。对第一种情况，WA=11,WB<10；现在来算A胜出此局的概率，并记为P1，由于最后一球必为A胜的，故在对战盘数n=WB+10下来讨论

Yn=X1+X2+…+Xn

P(Y=10)= g10(1-g)WB 其中WB=0,1,2,..9

由上式知，A可在WB=i,其中i=0,1,2,…,9的情况下胜出，由于之间是互斥的，所以概率可叠加，因此可得P1 ：

P1= gP(Y10+i=10)= g11(1-g)i

对于第二种情况下，亦即WB>=10,WA=WB+2，记A胜出此局的概率为P2，则前20球必为AB各胜10球(否则就是第一种情况了)，总球数n=WA+WB=2WB+2,即n=22,24,…,2k+2,…

A要胜出此局，则最后两球必为A赢的，对于每一n=2k+2，k>=10,我们考虑从第21球开始

的r=n-22球(包括第21球),A,B在这期间的胜负可以说是交替的,即可以把相邻两球作为一个整体,把这段期间作分割,如下:

(第21球,第22球 ),(第23球,第24球)…………….(第n-4球,第n-3球)

在每个分割中,A,B各胜一球.

A在不同球数下胜出的均是互斥的。故有

P2= g10(1-g)10 其中k=10,11,12,…

=

记F(k)= =2-11g (1-g)-1

由于g是概率，故0≤g≤1,那么1-g≥0，所以有0≤2g(1-g)≤ =

故 = ，记L=2g(1-g), t=2-11g (1-g)-1/(1-L)

则F(k)= t Lk ≤t(1/2)k

由此可知，P2为收敛级数，并且有P2=tL11=

现在，我们来看一下，A胜出此局的概率是多少？我们记之为P3。由于，A在不同球数胜出的是相互独立的，互斥的，所以有

P3=P1+P2

=

a,对于5盘3胜

用P4来记A胜的概率，则比赛的盘数n可为3,4,5

n=3时，概率为： (P3)3

n=4时，最后一盘必为A胜，故概率为：P3 (P3)2(1-P3)

n=5时，最后一盘也必为A胜，故概率为：P3 (P3)2(1-P3)2

于是有P4=(P3)3+ P3 (P3)2(1-P3)+ P3 (P3)2(1-P3)2=10(P3)3 – 15(P3)4+6(P3)5

b,对于7盘4胜

用P5来记A用的概率，则比赛的盘数n可为4,5,6,7

n=4时，概率为： (P3)4

n=5时，最后一盘必为A胜，故概率为：P3 (P3)3(1-P3)

n=6时，最后一盘也必为A胜，故概率为：P3 (P3)3(1-P3)2

n=7时，最后一盘也必为A胜，故概率为：P3 (P3)3(1-P3)3

于是有P5=(p3)4[-20(P3)3+70(P3)4-84P3+35]或P5=(p3)4[1+4(1-p3)+10(1-p3)2+20(1-p3)3]

二、现在来讨论21分制下A选手胜出的总的概率。

有了11分制的的讨论，21分制下将易得出如下结果，(其论证过程类似于11分制的论证程)

对应于11分制下的P3，我们有p3=

=

a,对于3盘2胜下A胜出的概率，对应于11分制下的P4，我们记之为p4，则有

p4=3(p3)2-2(p3)3

b,对于5盘3胜下A胜出的概率，对应于11分制下的P5，我们记之为p5,则有

p5=(p3)3[6(p3)2-15p3+10]

下面我们用Mathimatica来分别作出P4和p4，P5和p5的图象比较如下：

并以步长为0.025,计算出g从0到1,P4和p4，P5和p5的比较数据如下：

num g P4 p4 P5 p5

1 0.000 0.000 0.000 0.000 0.000

2 0.025 0.000 0.000 0.000 0.000

3 0.050 0.000 0.000 0.000 0.000

4 0.075 0.000 0.000 0.000 0.000

5 0.100 0.000 0.000 0.000 0.000

6 0.125 0.000 0.000 0.000 0.000

7 0.150 0.000 0.000 0.000 0.000

8 0.175 0.000 0.000 0.000 0.000

9 0.200 0.000 0.000 0.000 0.000

10 0.225 0.000 0.000 0.000 0.000

11 0.250 0.000 0.000 0.000 0.000

12 0.275 0.000 0.000 0.000 0.000

13 0.300 0.000 0.000 0.000 0.000

14 0.325 0.001 0.000 0.000 0.000

15 0.350 0.003 0.001 0.001 0.000

16 0.375 0.011 0.006 0.004 0.001

17 0.400 0.034 0.024 0.016 0.007

18 0.425 0.085 0.068 0.055 0.032

19 0.450 0.181 0.161 0.144 0.108

20 0.475 0.324 0.310 0.298 0.268

21 0.500 0.500 0.500 0.500 0.500

22 0.525 0.676 0.690 0.702 0.732

23 0.550 0.819 0.839 0.856 0.892

24 0.575 0.915 0.932 0.945 0.968

25 0.600 0.966 0.6 0.984 0.993

26 0.625 0.989 0.994 0.996 0.999

27 0.650 0.9 0.999 0.999 1.000

28 0.675 0.999 1.000 1.000 1.000

29 0.700 1.000 1.000 1.000 1.000

30 0.725 1.000 1.000 1.000 1.000

31 0.750 1.000 1.000 1.000 1.000

32 0.775 1.000 1.000 1.000 1.000

33 0.800 1.000 1.000 1.000 1.000

34 0.825 1.000 1.000 1.000 1.000

35 0.850 1.000 1.000 1.000 1.000

36 0.875 1.000 1.000 1.000 1.000

37 0.900 1.000 1.000 1.000 1.000

38 0.925 1.000 1.000 1.000 1.000

39 0.950 1.000 1.000 1.000 1.000

40 0.5 1.000 1.000 1.000 1.000

41 1.000 1.000 1.000 1.000 1.000

程序清单如下：

#include<stdio.h>

#include<stdlib.h>

#include<math.h>

double c(int i,int n){//返回组合数

if(i>n/2) i=n-i;

double s=1;

int k,j;

for(k=n,j=1;j<i+1;j++,k--)

s=s*k/j;

return s;

}

int main()

{

freopen("cmp.out","w",stdout);

int i=0,k=1;

double g,s,temp,p4=1,p5,pp4,pp5;//p4 为P4，pp4为p4，p5为P5，pp5为p5

s=0;temp=1;

printf("num g P4\t p4\t P5\t p5\n");

for(g=0.00;g<=1;g+=0.025){

s=0;temp=1;

for(i=0;i<10;i++){

s+=c(10,i+10)*temp*pow(g,11);

temp*=1-g;

}

s=s+c(10,20)*pow(g*(1-g),10)*g*g/(1-2*g*(1-g));//s为P3

p4=pow(s,3);

p5=p4*s;

p4=p4*(1+3*(1-s)+6*(1-s)*(1-s));

p5=p5*(1+4*(1-s)+10*(1-s)*(1-s)+20*(1-s)*(1-s)*(1-s));

s=0;temp=1;

for(i=0;i<20;i++){

s+=c(20,i+20)*temp;

temp*=1-g;

}

s*=pow(g,21);

s=s+c(20,40)*pow(g*(1-g),20)*g*g/(1-2*g*(1-g));//s为p3

pp4=s*s*(3-2*s);

pp5=s*s*s*(1+3*(1-s)+6*(1-s)*(1-s));

printf("%3d %.3lf %.3lf\t%.3lf\t%.3lf\t%.3lf\n",k++,g,p4,pp4,p5,pp5);

}

fclose(stdout);

return 0;

}

现在对图象与数据进行分析：

数据与图象是吻合的，图象是直观的，数据只是对图象的一个辅肋理解和有力佐证（因为细微的差别在图象上是较难发现的）。

现在我们来简单验证一下图象与数据的模拟效果如何。无论是在数据上还是图象上，一个很明显的特点就是赢的概率是g的增函数。容易看出，当选手的胜率g为0.5时，无论在哪一种情况下，他赢得本场比赛的概率均为0.5,相应地当g趋向0时，赢的概率也趋于0，g趋于1时，赢的概率也趋于1；这个与事实是相符合的，事实上当两人势均力敌时，当然哪一方赢的概率均为0.5；当某一方胜率g=0（或g=1）时，说明两个级别相差悬殊的选手在比赛，很明显，当然是优势的一方胜出的了，亦即无论是11分制还是21分制， “世界顶尖高手也纷纷被无名小卒淘汰，三四流选进决赛”的“偶然性”（概率），是趋近于零的。那么一流选手与二，三流之间的关系如何呢？

从图象和数据中，一流选手对阵二三流时，就是当胜率略大于0.5时的情形了，可以看出，在11分制下时，一流选手落败的“偶然性”比在21分制下落败的要大一点（数据上很明显了，图象上是21分制的概率曲线是在11分制的概率曲线之上的，说明在相同的胜率g下，21分制下该选手胜出比赛的概率要大）。这个也实际情况也是相符合的， “11分制的实行，使比赛增加偶然性增加，让一些二三流选手也有机会战胜一流选手”。这是因为11分制所用的赛程比21分制下的要短，所以优势一方相对不利。以上论述充分证明了拟合效果是可以接受的，模型是正确的。

也许，你会认为上述两个图象的概率曲线都较接近，差别不太明显，这是因为多盘比赛平均下来使得正负减弱，图象均衡，不妨来看一下单局时的情况，如下图所示，下图是一个仅表示一局的11分制和21分制下输赢概率的比较，亦即P3与p3的比较，差别比较明显。

本模型也证明了，11分制是可以接受的。因为它使比赛的“偶然性”增加，使比赛更加惊险，优势选手也稍弱的选手之间的竞技更具悬念，也就是说“有利于形成对抗激烈，场面精彩的比赛”；使比赛更吸引人，赛程的缩短也不会使观众因长时间观看而感到乏味，于是更多的观众会观看这些相对更惊险的比赛。同时比赛偶然性的增加，也使的更多弱势选手，乒乓球爱好者跃跃欲试，更勇敢地加入到比赛的行列中去，“运动就是这样推广开去的”。观众的增加，和对此项运动的热爱增加，将更有利于乒乓球市场的开发，赞助商的投入也回得到更大的回报，其产品，企业知明度将有所上升，更有利于他的利益。

II、综合模型

显然影响比赛结果的不会单单只有技术因素的，技术因素是最关键的因素，但是想要得到更好的模拟效果，我们还必需考虑更多，更全面才行！

现在，我们来分析一下影响选手们比赛结果的因素。

1， 技术因素，这个是关键，在I 中我们已详细讨论过了。

2， 心理因素，在这方面，我们可考虑选手们在处理问题时的能力，受影响的因素和处理关键球（决胜负的一球）时的能力问题，也就是选手受关键球影响的因素。

3， 进入状态的时间长短，有些选手很快进入状态，但有些却是慢热型的，11分制下与21分制下由于赛程的长短不一致，所以选手的慢热与否会影响比赛的结果

4， 发球权，有些选手在发球方面很讲技术，随着11分制由21分制的5球一换变成2球一换，这必然会对选手造成影响的。

5， 体力问题，由于选手们均是长期接受严格的训练，长期参赛的，所以，一般来说，双方的体力消耗都是同等下降的，故可看作等同的，所以可以忽略不作考虑。

根据上述因素，我们在I的基础上建立一个更加复杂，综合的模型。

仍旧拿A和B作考虑，A的胜率也还是记为g ,(由于B的也相应决定，为1-g，所以就不另作讨论了)。但是现在的g是要考虑到受其它因素影响的，是变动的，而不象I中单单受技术因素决定、恒定的。现在就来讨论一下g应如何表示吧。

g主要由技术因素决定，但是会随赛程的进展而变动。首先g还会受到影响。我们可定义g=g(i,j)，其中记A与B的得分分别为i和j,也就是说此时A、B的为i:j。令g0为A开始时的胜率(注意这个是赢球的概率，而不完全是技术水平反映，因为刚开始时，选手可能还没有进入状态)。现考虑选手进入状态的快慢对g的影响，记函数m(x),其中x=i+j，用m(x)来表A进入状态的快慢程度对g造成影响的调谐因子，于是有g(i,j)=g0*m(i+j)。显然当A比B快进入状态时0≤m(x)≤1,单调上升，因为随着比赛的进行，B越来越进入状态了，g慢慢减少。反之，若慢，则1≤m(x)，单调下降，因为随着赛事的进行，A越来越进入状态了，g慢慢增大，g增大的速度就会减慢。但无论m(x)是增还是降，最后均会趋于一定值，记为m0。不妨设当x=K时，m(x)=m0 。我们可记当选手进入稳定状态时g=g(i,j)m0 。

现在来考虑关键球对g的影响，前面已说过关键球其实就是决胜负的一球,我们把这一球对A、B方对输赢此球的影响用因子α表示。我们不妨用一函数w(i,j)来描述这种情况，当状态i:j时为可决定胜负时w(i,j)=α，否则w(i,j)=1(也就是对比赛无影响)。所以，现在可记g(i,j)=g0m(i+j)w(i,j)。

现在来考虑A输球数(输球数为负时，即赢球)对g的影响，现定义一函数L(x),其中x=i-j。显然当x>0时L(x)≥1,x=0时L(x)=1,x<0时，L(x)≤1。所以现在可记g(i,j)=g0m(i+j)w(i,j)L(i-j)。

最后，我们来考虑发球权对A的胜率g的影响，设当A获得发球权时，影响用β1表示，无发球权时，用β2表求。因为11分制下是2球一换的，所以我们用C来标记是否A最先发球，若是则C=0，否则C=1。那么A发球的充要条件是 mod(2)等于0，否则等于1。同理，在21分制下，若A发球的充要条件是 mod(2)等于0，否则等于1，这里C与上相同。所以可定义一函数F(x)，当x=0时,F(x)= β1 ,当x=1时，F(x)= β2 。这里，在11分制下x= mod(2) ，21分制下x= mod(2) 。

所以，现在可记g(i,j)=g0m(i+j)w(i,j)L(i-j)F(x),其中x的定义如上。

好了，分析到此为止，g的表示式最终确定了下来了：

g(i,j)=g0m(i+j)w(i,j)L(i-j)F(x) ，各函数和参量的定义上面都均已给出

g的讨论正式结束，现在让我们进入下一阶段的讨论吧，讨论A胜出比赛的概率。

我们不妨随着比赛的进程，用i:j ,来详细探讨吧。现令G(i,j)为到达i:j时的概率。由于i:j是相互独立的，亦即不同的为互斥，当i:j，不为最终状态时(就是胜负状态时)，到达此的可能由i-1:j或i:j-1达到的。因此可得G(i,j)

G(i,j)=g(i-1,j)G(i-1,j) i≥1,j=0

G(i,j)=(1-g(i,j-1))G(i,j-1) j≥1,i=0

G(i,j)=g(i-1,j)G(i-1,j)+(1-g(i,j-1))G(i,j-1) i,j≥1

当为胜负时，若A胜，亦即i>j,到达这状态的只可能为i-1:j ，所以这时有：G(i,j)=g(i-1,j)G(i-1,j)

若A输，亦即i<j, ,到达这状态的只可能为i:j-1 ，所以这时有：

G(i,j)=(1-g(i,j-1))G(i,j-1)

其中G(0,0)=1

我们可以作i,j的通达图如下，

注：图中的每一整点(i,j)，代表状态()i:j。本通达图还与上述概率公式是一致的，我们可定义整点(i,j)的大小为G(i,j)。则所有到达这个整点的路径经过的整点的大小之和就是这个整点的大小。

其中L1表示A胜，L2表示B胜，比赛进程在折线L1、L2和i,j轴内。把此范围内的所有点(不包含L1，L2上的点)的集合 定义为点集V。对图分析，对于L1上任一点(i,j)的G(i,j)均由(0，0)到(i,j)上不同路径传递过来的概率之和。

如上图，(i,j)为汇点，其它各点上的数值表示从这点到(i,j)的不同路径数目。

我们就可推出

lnG(i,j)=Kij (0,0) lnG(0,0) + 其中G(0,0)=1

=

其中，tij(x,y)为从(x,y)到(i,j)经过边(x,y)?(x+1,y)的路径数

t’ij(x,y)为从(x,y)到(i,j)经过边(x,y)?(x,y+1)的路径数

所以在11分制下，A胜出一局的概率为

P1= 其中L1为折线如上所述

在21分制下，同理有

P’1= 其中L’1的定义类似于L1，G’(i,j)的定义与G(i,j)一致(图略)

之后，我们取lnP1与lnP’1作比较，有

其中K1,K2i,j,K3i,j,K4i,j,K5i,j,r1,r2i,j,r3i,jr4i,j,r5i,j 均为常数

本模型的建立到此为止。由于篇幅有限，数据庞大，常细数据比较就不再细述了，详细的比较分析请看I 。I 的模型建立已足可解决本问题了，II 的深入探讨到此为止。

III 对乒乓球11分制的利弊的综合评价及建议

由本模型可以看出11分制是可以接受的。因为它使比赛的“偶然性”增加，使比赛更加惊险，优势选手与稍弱的选手之间的竞技更具悬念性，二三流选手打败一流选手进入决赛的可能性更大，更能吸引观众。既然二三流选手有了更大的可能击败一流选手进入决赛，那么他们必然会打得更加勇敢，更加尽心尽力，因为结果不再像以前那样“必败无疑”，所以信心增加了，且也无什么心理压力，斗志更盛；另一方面，一流选手落败的可能性也变大了，他们知道此时不能再像以前一样，能十拿九稳地获胜，因为21分制下就算是输了先手在后阶段还可补救，但现在11分制下就不可能了，于是打球也会更尽力，心理上就丝毫也不敢放松、马虎了，每一球都力求打败对手，否则自己很可能处境将会非常狼狈，甚至会被淘汰出局。于是比赛双方就会殊死对抗，全力以付，浑身解数了，比赛会因此会变得更加激烈，更加精彩。也就是说“有利于形成对抗激烈，场面精彩的比赛”；比赛更吸引人。同时21分制改成11分制后赛程的缩短也不会使观众因长时间观看而感到过度疲倦，乏味，于是更多的观众会观看这些相对更惊险的比赛。同时因为比赛偶然性的增加，也使的更多弱势选手，乒乓球爱好者跃跃欲试，更勇敢地加入到比赛的行列中去，同时这些爱好者还会把身边的亲朋戚友也拉入这一运动行列中来，而亲朋戚友们见这种运动是这么多人喜爱的，且比赛是非常精彩，可赏性相当高，也就当然愿意加入了。可见“运动就是这样推广开去的”。观众的增加，和人们对此项运动的热爱的增加，将更有利于乒乓球市场的开发，乒乓球相关产品的销量将更加大，会有更多的商家加入乒乓球相关的行业，使乒乓球的产品品种将更丰富，品牌间竞争将更大，产品质量将更加高，相关服务行业也将更加兴旺。赞助商们的投入也回得到更大的回报，其产品，企业知明度将有所上升，更有利于赞肋商们的利益。同时，更多的商家会注意到这个“广告”是值得做的，于是就会竞相出资出力赞肋，在这种竞争下，将更有利于，乒乓球赛事办得更好，更精彩。可见两者是相互促进的，互惠互利的。

但利弊是相对的，相生的，有利必有弊。11分制也会因其赛程太短，使得选手心理压力更大，2球一换使一些对发球依赖较大的老队员不得不提前退役。但是这些问题我们都可以克服的，选手们会很快地适应这些变化的。

建议选手们应加强锻炼，积极适应新的规则决定胜负的还主要是技术方面的因素，但同时也应加心理素质，减少心理方面对比赛造成的负面影响。

总体来说11分制利大于弊，是可行的，值得推广的，而不会像羽毛球7分制一样实行不久就取消。

征求2003年中山大学数学建模B题的报告论文(答案)

你是否了解怎么看羽毛球比赛？需要注意什么？

1要了解，第三视角和低角度的速率很不一样，后面一种更有利于学习培训。

2要了解，从技术上，技术专业女子单打才算是最合适业余组单打学习培训的目标。

3要了解，单打和双打基本上是这两种不一样健身运动，汤仙虎说：“单打是在奔波中实现技术，双打是在节奏快下进行技术！”

4要了解去留意，如何出球让敌人最不舒服，普遍的，例如单打：压两边道德底线，反复弹着点，杀吊融合，这些；例如双打：不随便起毛，杀中单接合部，打空档，集中化攻人——挑着弱的那一个打。

5要了解，无球时的挪动才算是真实反映能力的地区，双打尤其是。例如女双，应当尽可能轮换到女前男后的强有力攻击队型；例如男子双打，怎样补位，怎样维护，尤为重要。

6要了解，双打的真谛不取决于击败敌人，取决于维护好队友，例如同伴抢网，你需要维护好他的头上部位。

7要了解去留意，足球运动员是怎样一步一步把敌人迫使到搞出自身的优势球路；也去留意，足球运动员怎样解决处于被动。

8要了解去留意，双打怎样无痕接发，好的开球/无痕接发是获得这一球的一半；开球/无痕接发不太好，如同撒了一个谎，得用99个谎去填补。

9要了解，精彩镜头一般是严重的那一拍，可是，更有了解使用价值的，一般是致命性一拍的前两三拍，和致命性一拍的筹备姿势！

练球。练球就是指单一技术的反复训练，和出场打是两回事，一样是练球，一样投入时间，有的人提升快，有的人提升慢，一个很有可能的因素是，提升慢的人做的是反复训练，提升快的人做的是加固训练。

乒乓球新旧赛制对析

关键字：11分制 21分制

题目描述：

自2001年10月1日起，国际乒联改用11分制等新规则。11分制的实行，使比赛偶然性增加，让一些二三流选手也有机会战胜一流选手。“但这个偶然性应有个度，”王家声说：“如果这个偶然性大到世界顶尖高手也纷纷被无名小卒淘汰，三四流选进决赛，那它就不是好规则了。”，是否会象羽毛球7分制一样实行不久就取消呢？

请就乒乓球新旧赛制对析，试对11分制的5盘3胜与21分制的3盘2胜制作定量的比较分析；试对11分制的7盘5胜和21分制的5盘3胜制作定量的比较分析；请就是否有利于运动的推广；是否有利于形成对抗激烈，场面精彩的比赛；是否有利于它的市场开发和赞助商利益方面来评价乒乓球11分制利弊如何，并作出建议。

参量和函数说明：

I 中的如下：

A：选手一 B：选手二

WA:A胜的球数 WB: B胜的球数

g: A每球的胜率，即赢得一球的概率

P1: 11分制下，A胜出一局，且WA=11,WB<10时，的概率

P2：11分制下，A胜出一局，且 WB>=10,WA=WB+2时，的概率

P3：11分制下，A胜出一局的总概率

P4：11分制下，5盘3胜，A胜出的总概率

P5：11分制下，7盘4胜，A胜出的总概率

p3: 21分制下，A胜出一局的总概率

p4: 21分制下，3盘2胜，A胜出的概率

p5: 21分制下，5盘3胜，A胜出的概率

II 中的如下：

A：选手一 B：选手二

i:A的得分，赢球数 j:B的得分，赢球数 n:总球数

g(i,j): A在i:j下胜出一球的概率，是随赛程而变化的函数

g0：A刚开始时的胜率

m(x):来表A进入状态的快慢程度对g造成影响的调谐因子

α:关键球(决胜负的一球)对A方对输赢此球的影响的因子

w(i,j)：用来描述A方输赢在i:j下，赢得此球的因子函数，当状态i:j时为可决定胜负(关键球)时w(i,j)=α，否则w(i,j)=1(也就是对比赛无影响)

L(x)：A输球数(输球数为负时，即赢球)对g的影响的因子函数，其中x=i-j

C：用来来标记A是否最先发球，若是则C=0，否则C=1

F(x)：发球权对A的胜率g的影响的因子函数，其中在11分制下x= mod(2) ，21分制下x= mod(2) 。

G(i,j)：到达i:j时的概率

L1：表示A胜的折线 L2：表示B胜的折线

P1：在11分制下，A胜出一局的概率 P’1：在21分制下，A胜出一局的概率

解答过程：

I,初步建模

我们不妨先建立一个两选手对战的模型，且作出以下规定：1,根据两选手的技术水平，给定他们每一球胜出的概率；2，设这种概率是恒定不变的，也就是说不考虑其它因素的影响。

现有两选手A和B对战，我们现在只拿出一个选手出来作考虑，比如A，因为比赛双方是相对的，确定了A的胜率，B胜率也随之确定(等于1减去A的胜率)。记A赢球为标志1，输球为标志为0，则概率空间X={0,1}。设比赛共打了n球，则由前面的设易知，存在服从0-1分布的n个相互独立的随机变数x1,x2,x3,…,xn ，其中xi∈X,i=1,2,..,n。

设A每球的胜率为g(相应地B的胜率为1-g)，对战n盘，有Y=X1+X2+…+Xn ,服从两项分布ψ(n,g).

一、现在我们先来讨论11分制下A选手胜出的总的概率。

由于在每一局中，只有当A先胜出B至少两球，且打足11球时，A方可赢得这一局。

这样说来，我们可分两种情况来讨论，一是A先胜出11球，且B胜出的不足10球，则A就可胜出了。二是，B超过或等于10球，这时当且仅当A领先出两球时，A才可赢得本局。

记A胜的球数为WA，B的为WB。对第一种情况，WA=11,WB<10；现在来算A胜出此局的概率，并记为P1，由于最后一球必为A胜的，故在对战盘数n=WB+10下来讨论

Yn=X1+X2+…+Xn

P(Y=10)= g10(1-g)WB 其中WB=0,1,2,..9

由上式知，A可在WB=i,其中i=0,1,2,…,9的情况下胜出，由于之间是互斥的，所以概率可叠加，因此可得P1 ：

P1= gP(Y10+i=10)= g11(1-g)i

对于第二种情况下，亦即WB>=10,WA=WB+2，记A胜出此局的概率为P2，则前20球必为AB各胜10球(否则就是第一种情况了)，总球数n=WA+WB=2WB+2,即n=22,24,…,2k+2,…

A要胜出此局，则最后两球必为A赢的，对于每一n=2k+2，k>=10,我们考虑从第21球开始

的r=n-22球(包括第21球),A,B在这期间的胜负可以说是交替的,即可以把相邻两球作为一个整体,把这段期间作分割,如下:

(第21球,第22球 ),(第23球,第24球)…………….(第n-4球,第n-3球)

在每个分割中,A,B各胜一球.

A在不同球数下胜出的均是互斥的。故有

P2= g10(1-g)10 其中k=10,11,12,…

=

记F(k)= =2-11g (1-g)-1

由于g是概率，故0≤g≤1,那么1-g≥0，所以有0≤2g(1-g)≤ =

故 = ，记L=2g(1-g), t=2-11g (1-g)-1/(1-L)

则F(k)= t Lk ≤t(1/2)k

由此可知，P2为收敛级数，并且有P2=tL11=

现在，我们来看一下，A胜出此局的概率是多少？我们记之为P3。由于，A在不同球数胜出的是相互独立的，互斥的，所以有

P3=P1+P2

=

a,对于5盘3胜

用P4来记A胜的概率，则比赛的盘数n可为3,4,5

n=3时，概率为： (P3)3

n=4时，最后一盘必为A胜，故概率为：P3 (P3)2(1-P3)

n=5时，最后一盘也必为A胜，故概率为：P3 (P3)2(1-P3)2

于是有P4=(P3)3+ P3 (P3)2(1-P3)+ P3 (P3)2(1-P3)2=10(P3)3 – 15(P3)4+6(P3)5

b,对于7盘4胜

用P5来记A用的概率，则比赛的盘数n可为4,5,6,7

n=4时，概率为： (P3)4

n=5时，最后一盘必为A胜，故概率为：P3 (P3)3(1-P3)

n=6时，最后一盘也必为A胜，故概率为：P3 (P3)3(1-P3)2

n=7时，最后一盘也必为A胜，故概率为：P3 (P3)3(1-P3)3

于是有P5=(p3)4[-20(P3)3+70(P3)4-84P3+35]或P5=(p3)4[1+4(1-p3)+10(1-p3)2+20(1-p3)3]

二、现在来讨论21分制下A选手胜出的总的概率。

有了11分制的的讨论，21分制下将易得出如下结果，(其论证过程类似于11分制的论证程)

对应于11分制下的P3，我们有p3=

=

a,对于3盘2胜下A胜出的概率，对应于11分制下的P4，我们记之为p4，则有

p4=3(p3)2-2(p3)3

b,对于5盘3胜下A胜出的概率，对应于11分制下的P5，我们记之为p5,则有

p5=(p3)3[6(p3)2-15p3+10]

下面我们用Mathimatica来分别作出P4和p4，P5和p5的图象比较如下：

并以步长为0.025,计算出g从0到1,P4和p4，P5和p5的比较数据如下：

num g P4 p4 P5 p5

1 0.000 0.000 0.000 0.000 0.000

2 0.025 0.000 0.000 0.000 0.000

3 0.050 0.000 0.000 0.000 0.000

4 0.075 0.000 0.000 0.000 0.000

5 0.100 0.000 0.000 0.000 0.000

6 0.125 0.000 0.000 0.000 0.000

7 0.150 0.000 0.000 0.000 0.000

8 0.175 0.000 0.000 0.000 0.000

9 0.200 0.000 0.000 0.000 0.000

10 0.225 0.000 0.000 0.000 0.000

11 0.250 0.000 0.000 0.000 0.000

12 0.275 0.000 0.000 0.000 0.000

13 0.300 0.000 0.000 0.000 0.000

14 0.325 0.001 0.000 0.000 0.000

15 0.350 0.003 0.001 0.001 0.000

16 0.375 0.011 0.006 0.004 0.001

17 0.400 0.034 0.024 0.016 0.007

18 0.425 0.085 0.068 0.055 0.032

19 0.450 0.181 0.161 0.144 0.108

20 0.475 0.324 0.310 0.298 0.268

21 0.500 0.500 0.500 0.500 0.500

22 0.525 0.676 0.690 0.702 0.732

23 0.550 0.819 0.839 0.856 0.892

24 0.575 0.915 0.932 0.945 0.968

25 0.600 0.966 0.6 0.984 0.993

26 0.625 0.989 0.994 0.996 0.999

27 0.650 0.9 0.999 0.999 1.000

28 0.675 0.999 1.000 1.000 1.000

29 0.700 1.000 1.000 1.000 1.000

30 0.725 1.000 1.000 1.000 1.000

31 0.750 1.000 1.000 1.000 1.000

32 0.775 1.000 1.000 1.000 1.000

33 0.800 1.000 1.000 1.000 1.000

34 0.825 1.000 1.000 1.000 1.000

35 0.850 1.000 1.000 1.000 1.000

36 0.875 1.000 1.000 1.000 1.000

37 0.900 1.000 1.000 1.000 1.000

38 0.925 1.000 1.000 1.000 1.000

39 0.950 1.000 1.000 1.000 1.000

40 0.5 1.000 1.000 1.000 1.000

41 1.000 1.000 1.000 1.000 1.000

程序清单如下：

#include<stdio.h>

#include<stdlib.h>

#include<math.h>

double c(int i,int n){//返回组合数

if(i>n/2) i=n-i;

double s=1;

int k,j;

for(k=n,j=1;j<i+1;j++,k--)

s=s*k/j;

return s;

}

int main()

{

freopen("cmp.out","w",stdout);

int i=0,k=1;

double g,s,temp,p4=1,p5,pp4,pp5;//p4 为P4，pp4为p4，p5为P5，pp5为p5

s=0;temp=1;

printf("num g P4\t p4\t P5\t p5\n");

for(g=0.00;g<=1;g+=0.025){

s=0;temp=1;

for(i=0;i<10;i++){

s+=c(10,i+10)*temp*pow(g,11);

temp*=1-g;

}

s=s+c(10,20)*pow(g*(1-g),10)*g*g/(1-2*g*(1-g));//s为P3

p4=pow(s,3);

p5=p4*s;

p4=p4*(1+3*(1-s)+6*(1-s)*(1-s));

p5=p5*(1+4*(1-s)+10*(1-s)*(1-s)+20*(1-s)*(1-s)*(1-s));

s=0;temp=1;

for(i=0;i<20;i++){

s+=c(20,i+20)*temp;

temp*=1-g;

}

s*=pow(g,21);

s=s+c(20,40)*pow(g*(1-g),20)*g*g/(1-2*g*(1-g));//s为p3

pp4=s*s*(3-2*s);

pp5=s*s*s*(1+3*(1-s)+6*(1-s)*(1-s));

printf("%3d %.3lf %.3lf\t%.3lf\t%.3lf\t%.3lf\n",k++,g,p4,pp4,p5,pp5);

}

fclose(stdout);

return 0;

}

现在对图象与数据进行分析：

数据与图象是吻合的，图象是直观的，数据只是对图象的一个辅肋理解和有力佐证（因为细微的差别在图象上是较难发现的）。

现在我们来简单验证一下图象与数据的模拟效果如何。无论是在数据上还是图象上，一个很明显的特点就是赢的概率是g的增函数。容易看出，当选手的胜率g为0.5时，无论在哪一种情况下，他赢得本场比赛的概率均为0.5,相应地当g趋向0时，赢的概率也趋于0，g趋于1时，赢的概率也趋于1；这个与事实是相符合的，事实上当两人势均力敌时，当然哪一方赢的概率均为0.5；当某一方胜率g=0（或g=1）时，说明两个级别相差悬殊的选手在比赛，很明显，当然是优势的一方胜出的了，亦即无论是11分制还是21分制， “世界顶尖高手也纷纷被无名小卒淘汰，三四流选进决赛”的“偶然性”（概率），是趋近于零的。那么一流选手与二，三流之间的关系如何呢？

从图象和数据中，一流选手对阵二三流时，就是当胜率略大于0.5时的情形了，可以看出，在11分制下时，一流选手落败的“偶然性”比在21分制下落败的要大一点（数据上很明显了，图象上是21分制的概率曲线是在11分制的概率曲线之上的，说明在相同的胜率g下，21分制下该选手胜出比赛的概率要大）。这个也实际情况也是相符合的， “11分制的实行，使比赛增加偶然性增加，让一些二三流选手也有机会战胜一流选手”。这是因为11分制所用的赛程比21分制下的要短，所以优势一方相对不利。以上论述充分证明了拟合效果是可以接受的，模型是正确的。

也许，你会认为上述两个图象的概率曲线都较接近，差别不太明显，这是因为多盘比赛平均下来使得正负减弱，图象均衡，不妨来看一下单局时的情况，如下图所示，下图是一个仅表示一局的11分制和21分制下输赢概率的比较，亦即P3与p3的比较，差别比较明显。

本模型也证明了，11分制是可以接受的。因为它使比赛的“偶然性”增加，使比赛更加惊险，优势选手也稍弱的选手之间的竞技更具悬念，也就是说“有利于形成对抗激烈，场面精彩的比赛”；使比赛更吸引人，赛程的缩短也不会使观众因长时间观看而感到乏味，于是更多的观众会观看这些相对更惊险的比赛。同时比赛偶然性的增加，也使的更多弱势选手，乒乓球爱好者跃跃欲试，更勇敢地加入到比赛的行列中去，“运动就是这样推广开去的”。观众的增加，和对此项运动的热爱增加，将更有利于乒乓球市场的开发，赞助商的投入也回得到更大的回报，其产品，企业知明度将有所上升，更有利于他的利益。

II、综合模型

显然影响比赛结果的不会单单只有技术因素的，技术因素是最关键的因素，但是想要得到更好的模拟效果，我们还必需考虑更多，更全面才行！

现在，我们来分析一下影响选手们比赛结果的因素。

1， 技术因素，这个是关键，在I 中我们已详细讨论过了。

2， 心理因素，在这方面，我们可考虑选手们在处理问题时的能力，受影响的因素和处理关键球（决胜负的一球）时的能力问题，也就是选手受关键球影响的因素。

3， 进入状态的时间长短，有些选手很快进入状态，但有些却是慢热型的，11分制下与21分制下由于赛程的长短不一致，所以选手的慢热与否会影响比赛的结果

4， 发球权，有些选手在发球方面很讲技术，随着11分制由21分制的5球一换变成2球一换，这必然会对选手造成影响的。

5， 体力问题，由于选手们均是长期接受严格的训练，长期参赛的，所以，一般来说，双方的体力消耗都是同等下降的，故可看作等同的，所以可以忽略不作考虑。

根据上述因素，我们在I的基础上建立一个更加复杂，综合的模型。

仍旧拿A和B作考虑，A的胜率也还是记为g ,(由于B的也相应决定，为1-g，所以就不另作讨论了)。但是现在的g是要考虑到受其它因素影响的，是变动的，而不象I中单单受技术因素决定、恒定的。现在就来讨论一下g应如何表示吧。

g主要由技术因素决定，但是会随赛程的进展而变动。首先g还会受到影响。我们可定义g=g(i,j)，其中记A与B的得分分别为i和j,也就是说此时A、B的为i:j。令g0为A开始时的胜率(注意这个是赢球的概率，而不完全是技术水平反映，因为刚开始时，选手可能还没有进入状态)。现考虑选手进入状态的快慢对g的影响，记函数m(x),其中x=i+j，用m(x)来表A进入状态的快慢程度对g造成影响的调谐因子，于是有g(i,j)=g0*m(i+j)。显然当A比B快进入状态时0≤m(x)≤1,单调上升，因为随着比赛的进行，B越来越进入状态了，g慢慢减少。反之，若慢，则1≤m(x)，单调下降，因为随着赛事的进行，A越来越进入状态了，g慢慢增大，g增大的速度就会减慢。但无论m(x)是增还是降，最后均会趋于一定值，记为m0。不妨设当x=K时，m(x)=m0 。我们可记当选手进入稳定状态时g=g(i,j)m0 。

现在来考虑关键球对g的影响，前面已说过关键球其实就是决胜负的一球,我们把这一球对A、B方对输赢此球的影响用因子α表示。我们不妨用一函数w(i,j)来描述这种情况，当状态i:j时为可决定胜负时w(i,j)=α，否则w(i,j)=1(也就是对比赛无影响)。所以，现在可记g(i,j)=g0m(i+j)w(i,j)。

现在来考虑A输球数(输球数为负时，即赢球)对g的影响，现定义一函数L(x),其中x=i-j。显然当x>0时L(x)≥1,x=0时L(x)=1,x<0时，L(x)≤1。所以现在可记g(i,j)=g0m(i+j)w(i,j)L(i-j)。

最后，我们来考虑发球权对A的胜率g的影响，设当A获得发球权时，影响用β1表示，无发球权时，用β2表求。因为11分制下是2球一换的，所以我们用C来标记是否A最先发球，若是则C=0，否则C=1。那么A发球的充要条件是 mod(2)等于0，否则等于1。同理，在21分制下，若A发球的充要条件是 mod(2)等于0，否则等于1，这里C与上相同。所以可定义一函数F(x)，当x=0时,F(x)= β1 ,当x=1时，F(x)= β2 。这里，在11分制下x= mod(2) ，21分制下x= mod(2) 。

所以，现在可记g(i,j)=g0m(i+j)w(i,j)L(i-j)F(x),其中x的定义如上。

好了，分析到此为止，g的表示式最终确定了下来了：

g(i,j)=g0m(i+j)w(i,j)L(i-j)F(x) ，各函数和参量的定义上面都均已给出

g的讨论正式结束，现在让我们进入下一阶段的讨论吧，讨论A胜出比赛的概率。

我们不妨随着比赛的进程，用i:j ,来详细探讨吧。现令G(i,j)为到达i:j时的概率。由于i:j是相互独立的，亦即不同的为互斥，当i:j，不为最终状态时(就是胜负状态时)，到达此的可能由i-1:j或i:j-1达到的。因此可得G(i,j)

G(i,j)=g(i-1,j)G(i-1,j) i≥1,j=0

G(i,j)=(1-g(i,j-1))G(i,j-1) j≥1,i=0

G(i,j)=g(i-1,j)G(i-1,j)+(1-g(i,j-1))G(i,j-1) i,j≥1

当为胜负时，若A胜，亦即i>j,到达这状态的只可能为i-1:j ，所以这时有：G(i,j)=g(i-1,j)G(i-1,j)

若A输，亦即i<j, ,到达这状态的只可能为i:j-1 ，所以这时有：

G(i,j)=(1-g(i,j-1))G(i,j-1)

其中G(0,0)=1

我们可以作i,j的通达图如下，

注：图中的每一整点(i,j)，代表状态()i:j。本通达图还与上述概率公式是一致的，我们可定义整点(i,j)的大小为G(i,j)。则所有到达这个整点的路径经过的整点的大小之和就是这个整点的大小。

其中L1表示A胜，L2表示B胜，比赛进程在折线L1、L2和i,j轴内。把此范围内的所有点(不包含L1，L2上的点)的集合 定义为点集V。对图分析，对于L1上任一点(i,j)的G(i,j)均由(0，0)到(i,j)上不同路径传递过来的概率之和。

如上图，(i,j)为汇点，其它各点上的数值表示从这点到(i,j)的不同路径数目。

我们就可推出

lnG(i,j)=Kij (0,0) lnG(0,0) + 其中G(0,0)=1

=

其中，tij(x,y)为从(x,y)到(i,j)经过边(x,y)?(x+1,y)的路径数

t’ij(x,y)为从(x,y)到(i,j)经过边(x,y)?(x,y+1)的路径数

所以在11分制下，A胜出一局的概率为

P1= 其中L1为折线如上所述

在21分制下，同理有

P’1= 其中L’1的定义类似于L1，G’(i,j)的定义与G(i,j)一致(图略)

之后，我们取lnP1与lnP’1作比较，有

其中K1,K2i,j,K3i,j,K4i,j,K5i,j,r1,r2i,j,r3i,jr4i,j,r5i,j 均为常数

本模型的建立到此为止。由于篇幅有限，数据庞大，常细数据比较就不再细述了，详细的比较分析请看I 。I 的模型建立已足可解决本问题了，II 的深入探讨到此为止。

III 对乒乓球11分制的利弊的综合评价及建议

由本模型可以看出11分制是可以接受的。因为它使比赛的“偶然性”增加，使比赛更加惊险，优势选手与稍弱的选手之间的竞技更具悬念性，二三流选手打败一流选手进入决赛的可能性更大，更能吸引观众。既然二三流选手有了更大的可能击败一流选手进入决赛，那么他们必然会打得更加勇敢，更加尽心尽力，因为结果不再像以前那样“必败无疑”，所以信心增加了，且也无什么心理压力，斗志更盛；另一方面，一流选手落败的可能性也变大了，他们知道此时不能再像以前一样，能十拿九稳地获胜，因为21分制下就算是输了先手在后阶段还可补救，但现在11分制下就不可能了，于是打球也会更尽力，心理上就丝毫也不敢放松、马虎了，每一球都力求打败对手，否则自己很可能处境将会非常狼狈，甚至会被淘汰出局。于是比赛双方就会殊死对抗，全力以付，浑身解数了，比赛会因此会变得更加激烈，更加精彩。也就是说“有利于形成对抗激烈，场面精彩的比赛”；比赛更吸引人。同时21分制改成11分制后赛程的缩短也不会使观众因长时间观看而感到过度疲倦，乏味，于是更多的观众会观看这些相对更惊险的比赛。同时因为比赛偶然性的增加，也使的更多弱势选手，乒乓球爱好者跃跃欲试，更勇敢地加入到比赛的行列中去，同时这些爱好者还会把身边的亲朋戚友也拉入这一运动行列中来，而亲朋戚友们见这种运动是这么多人喜爱的，且比赛是非常精彩，可赏性相当高，也就当然愿意加入了。可见“运动就是这样推广开去的”。观众的增加，和人们对此项运动的热爱的增加，将更有利于乒乓球市场的开发，乒乓球相关产品的销量将更加大，会有更多的商家加入乒乓球相关的行业，使乒乓球的产品品种将更丰富，品牌间竞争将更大，产品质量将更加高，相关服务行业也将更加兴旺。赞助商们的投入也回得到更大的回报，其产品，企业知明度将有所上升，更有利于赞肋商们的利益。同时，更多的商家会注意到这个“广告”是值得做的，于是就会竞相出资出力赞肋，在这种竞争下，将更有利于，乒乓球赛事办得更好，更精彩。可见两者是相互促进的，互惠互利的。

但利弊是相对的，相生的，有利必有弊。11分制也会因其赛程太短，使得选手心理压力更大，2球一换使一些对发球依赖较大的老队员不得不提前退役。但是这些问题我们都可以克服的，选手们会很快地适应这些变化的。

建议选手们应加强锻炼，积极适应新的规则决定胜负的还主要是技术方面的因素，但同时也应加心理素质，减少心理方面对比赛造成的负面影响。

总体来说11分制利大于弊，是可行的，值得推广的，而不会像羽毛球7分制一样实行不久就取消。

2003年6月15日，解答毕